Definição: $ x_0$ é um ponto ordinário da equação

$\displaystyle y''+P(x)\,y'+Q(x)\,y=0$ (1)

se $ P(x)$ e $ Q(x)$ são funções analíticas no ponto $ x_0$. Caso contrário dizemos que $ x_0$ é um ponto singular.

Teorema: Seja $ x_0$ um ponto ordinário da equação (1), com $ \displaystyle\,P(x)=\sum_{n=0}^\infty p_n\,(x-x_0)^n\,$ e $ \displaystyle\,Q(x)=\sum_{n=0}^\infty q_n\,(x-x_0)^n\,$ com raios de convergência respectivamente $ R_1$ e $ R_2$. Então qualquer problema de valor inicial para a equação (1)

$\displaystyle \left\{ \begin{array}{l} y''+P(x)\,y'+Q(x)\,y=0 \\ y(x_0)=a_0 \ , \ \ y'(x_0)=a_1 \rule{0.cm}{0.5cm} \end{array} \right. $

tem solução única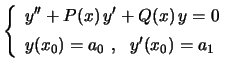 $ \displaystyle\,y(x)=\sum_{n=0}^\infty a_n\,(x-x_0)^n\,$, que é analítica no ponto $ x_0$ e tem raio de convergência $ R\geq\min\{R_1,R_2\}$.

Exemplo: Equação de Chebyshev

$\displaystyle (1-x^2)\,y''-x\,y'+\alpha^2y=0 \ , \quad \alpha={\rm const.} $

Para colocar a equação em forma normal, devemos dividir por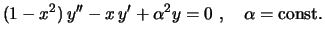 $ 1-x^2$. Portanto $ \displaystyle\,P(x)=\frac{-x}{1-x^2}\,$ e $ \displaystyle\,Q(x)=\frac{\alpha^2}{1-x^2}\,$. Logo 1 e $ -1$ são os únicos pontos singulares. Considerando $ \,x_0=0\,$, o teorema nos diz que vamos encontrar soluções da forma $ \displaystyle\,y(x)=\sum_{n=0}^\infty a_n\,x^n\,$ com raio de convergência $ R\geq1$.