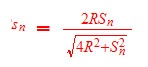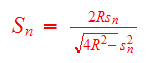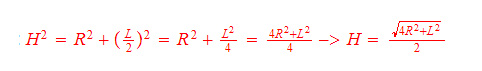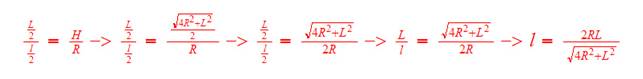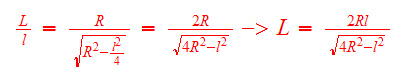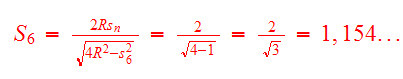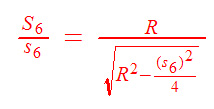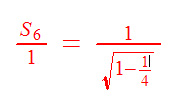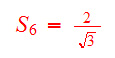Dedução 1

1) Se s_n denota o lado de um polígono regular de n lados inscrito num círculo de raio R, mostre que

2) Se S_n denota o lado de um polígono regular circunscrito a um círculo de raio R, mostre que

Resolução:

Tendo dois polígonos regulares de n lados, um inscrito e outro circunscrito a um círculo podemos obter a medida do lado de um a partir da medida do lado do outro.

1º) Tendo a medida do lado do polígono de lado L, circunscrito num círculo de raio R, pode-se relacionar L com l (lado do polígono inscrito de n lados).

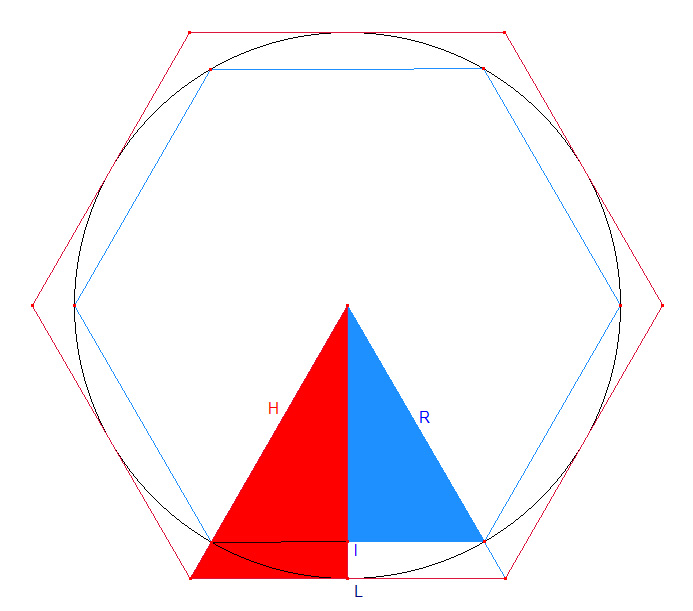
Observando a figura obtemos a seguinte relação:

Na figura, é fácil ver que os triângulos vermelho e azul são semelhantes.

Por semelhança de triângulos temos que:

.................................................................

2º) Tendo a medida do lado do polígono inscrito, novamente por semelhança de triângulos, temos:

Voltando ao cálculo de Arquimedes.

Sabendo s₆(lado do hexágono inscrito no círculo de raio 1), calculamos S₆ (lado do hexàgono circunscrito no círculo de raio 1).

De outro modo, por semelhança de triângulos temos:

 Voltar>>